Given,
The maximum acceleration that the rover can handle, a=0.513 m/s²
(A)
The rover slides down the ramp under the influence of gravity. The component of the gravity that provides the rover with the required acceleration is the component that is along the ramp.
Thus,
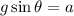
Where g is the acceleration due to gravity and θ is the angle of inclination of the ramp.
On substituting the known values,
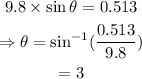
Thus the maximum angle that the ramp can be made with the horizontal is 3°
(B)
Given, the mass of the rover, m=1025 kg
The normal force will be equal to the vertical component of the weight of the rover.
That is,
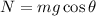
On substituting the known values,
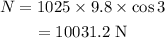
Thus the normal force on the rover is 10031.2 N