Question

Which of the following quadratic functions has a graph that opens downward? Check all that apply. A v=Bx2- 8x– 13 B. v= - (3+x? e. v=zx2 - 13x+5 O d. v=2r-

Answer 1

Ok, so

Remember that:

For any quadratic equation of the form:

`y=ax^2+bx+c`

- If the leading coefficient is greater than zero, the parabola opens upward, and

- If the leading coefficient is less than zero, the parabola opens downward.

So, here we have the following functions:

`v=(1)/(3)x^2-8x-13`

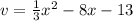
The leading coefficient is greater than zero, so this parabola opens upward.

Option B:

`\begin{gathered} v=-(3+x^2) \\ v=-x^2-3 \end{gathered}`

The leading coefficient is less than zero, so this parabola opens downward.

Option C:

`v=(2)/(3)x^2-13x+5`

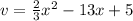
The leading coefficient is greater than zero, so this parabola opens upward.

Option D:

`v=2x-x^2`

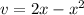
The leading coefficient is less than zero, so this parabola opens downward.

Therefore, the correct options are B and D.