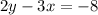Question

N N Which of the following is an equation of line k in the xy-plane above? (A) y=-x-4 (B) y = x+2 (C) 2y - 3x = -8 (D) 2y - 3x = -4

Answer 1

`2y-3x=-8`

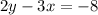
Step-by-step explanation:

Given the graph in the attached image;

The intercept of the line on the y-axis is at;

`\begin{gathered} y=-4 \\ At\text{ point;} \\ (0,-4) \\ \text{ intercept b is;} \\ b=-4 \end{gathered}`

At the x=2, the value of y is;

`\begin{gathered} y=-1 \\ at\text{ point;} \\ (2,-1) \\ \end{gathered}`

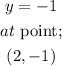
The slope of the line can be calculated using the two points on the graph;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(-1-(-4))/(2-0)=(-1+4)/(2) \\ m=(3)/(2) \end{gathered}`

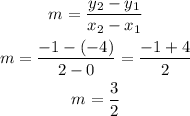
The slope intercept equation of a straight line is of the form;

`y=mx+b`

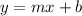
substituting the slope m and intercept b we have;

`y=(3)/(2)x-4`

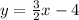
As this is not among the given options, let us solve further;

multiply through by 2 and move the x term to the left side;

`\begin{gathered} y(2)=(3)/(2)x(2)-4(2) \\ 2y=3x-8 \\ 2y-3x=-8 \end{gathered}`

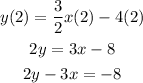
Therefore, from the given options the correct equation for the line is C;

`2y-3x=-8`