Question

A chef is going to use a mixture of two brands of Italian dressing. The first brand contains 8% vinegar, and the second brand contains 13% vinegar. The chef wants to make 230 milliliters of a dressing that is 11% vinegar. How much of each brand should she use?First brand:Second brand:Solve by percent mixture using system of linear equations.

Answer 1

We have to blend two brands of dressing with different proportions of vinegar. We want to obtain a mix of 230 cubic milimiters with a proportion of 11% of vinegar.

We can call A to the amount of dressing with 8% vinegar and B the amount of dressing with 13% vinegar.

Then, if the volume of the mix is 230 mm³, we can write:

`A+B=230`

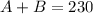
We can obtain another equation by looking at the amount of vinegar in the mix.

The amount will be the volume of the mix (230 mm³) times the proportion of vinegar (11% or 0.11 in decimal).

This amount of vinegar will be contributed by the vinegar of each brand. The first brand will contribute with a volume of A times 0.08 and the second brand will contribute with B times 0.13.

We can write this as a equation like this:

`\begin{gathered} 0.08*A+0.13*B=230*0.11 \\ 0.08A+0.13B=25.3 \end{gathered}`

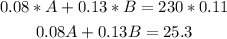
We now have a system of linear equations (two equations and two unknowns).

We can replace B from the second equation by using the first equation:

`\begin{gathered} A+B=230 \\ \Rightarrow B=230-A \end{gathered}`
`\begin{gathered} 0.08A+0.13B=25.3 \\ 0.08A+0.13(230-A)=25.3 \\ 0.08A+29.9-0.13A=25.3 \\ (0.08-0.13)A=25.3-29.9 \\ -0.05A=-4.6 \\ A=(4.6)/(0.05) \\ A=92 \end{gathered}`

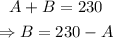
Knowing A = 92 mm³, we can find B as:

`\begin{gathered} B=230-A \\ B=230-92 \\ B=138 \end{gathered}`

Answer:

First brand: 92 mm³

Second brand: 138 mm³