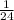Question

Given that a randomly chosen card from a standard deck of 52 cards is less than 7, what is the probability it is the 5 of diamonds? Assume that aces are low cards.

Answer 1

Step-by-step explanation: answers 27.6%

Answer 2

The picture below shows the whole 52 standard deck

Let B denotes the events of cards that is less than 7

We will include the aces in the set B, because we are told to assume that they are low cards

B = {all 2, all 3, all 4, all 5, all 6, all aces}

n(B) = 24

Let A denotes the events of cards that is a 5 of diamonds

A = {5diamond}

n(A) = 1

A n B = {5diamonds}

n(A n B) = 1

The probability

`\begin{gathered} p(A\cap B)=(1)/(52) \\ p(B)=(24)/(52) \end{gathered}`

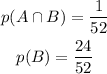
Note: Conditional Probability Formula

`p(A|B)=(p(A\cap B))/(p(B))`

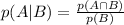
From the question, we want to find the probability of A given B

`\begin{gathered} p(A|B)=(p(A\cap B))/(p(B)) \\ p(A|B)=((1)/(52))/((24)/(52)) \\ p(A|B)=(1)/(52)*(52)/(24) \\ p(A|B)=(1)/(24) \end{gathered}`

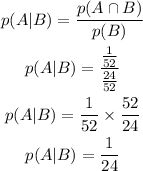
Therefore, the answer is

`(1)/(24)`