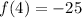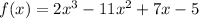
To find f(4) you divide the given polynomial into (x-4):
To divide:
1. Divide the first term of the dividend by the highest term of the divisor:
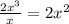
2. Multiply the divisor by the result:
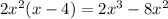
3. Substract the product in step 2 from the appropiat terms of the dividend (when you substract the symbols change) (then bring down the next term from the dividend)
4. Repeat previous steps:
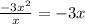
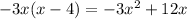
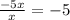
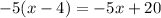
As the remainder is -25: