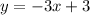Question

Write the equation of a line through (2, -3), perpendicular to y = 1/3x

Answer 1

to make a perpendicular function from another we must take its slope and make two transformations

the slope of y=1/3x is 1/3

the transformations:

1.

reverse the number

`(1)/(3)\longrightarrow(3)/(1)=3`

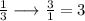
2.

and change the sign

`3\longrightarrow-3`

ok we have the slope now need the general equation of the line

`y=mx+b`

where m is the slope , b a cut point and (x,y) a point

so, we have the slope=-3 , and the point (2,-3) we can replace to find b

`\begin{gathered} (-3)=(-3)(2)+b \\ -3=-6+b \\ b=-3+6 \\ b=3 \end{gathered}`

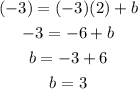
now we can replace b and the slope to have the final equation

`y=-3x+3`