Question

A rocket is fired upward from some initial distance above the ground. Its height (in feet), h, above the ground t seconds after it is fired is given by h(t)=-16t²+80t+2400What is the rocket's maximum height? feetHow long does it take for the rocket to reach its maximum height? secondsAfter it is fired, the rocket reaches the ground at t= seconds

Answer 1

`\begin{gathered} 2500ft \\ 12.5\:seconds \\ 25\:seconds \end{gathered}`

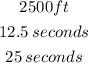
1) Let's find the maximum point of this quadratic equation, by using the following formula to get the h coordinate of the vertex and then plug into the function the value we found.

`\begin{gathered} y=-16t^2+80t+2400 \\ h=-(b)/(2a)=(-80)/(2(-16))=(5)/(2)=2.5 \\ k=-16((5)/(2))^2+80((5)/(2))+2400 \\ k=-16\cdot(25)/(4)+200+2400 \\ k=2500 \end{gathered}`

So the maximum height is given y the point at the vertex (2.5,2500) .i.e. 2500 feet

2) From the previous part, we can tell It takes 12.5 seconds for the rocket to get 2500 ft high.

`15-(-10)=(25)/(2)=12.5`

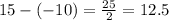
We are considering the rocket to strt flying off at x=-10.

3) To find when the rocket reaches the ground is to find the roots of this quadratic equation, and then pick one of them. So let's do it:

`\begin{gathered} -16t^2+80t+2400\:=0 \\ t=(-80\pm√(80^2-4\left(-16\right)\cdot\:2400))/(2\left(-16\right)) \\ t_1=(-80+400)/(2\left(-16\right))=-10 \\ t_2=(-80-400)/(2(-16))=15 \end{gathered}`

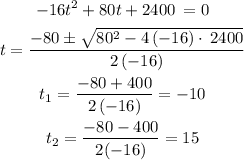
Since we cannot deal with the negative measurement of time. We can tell that

Note that the question is after it is fired consider the rocket is fired at x=-15 and hits its peak 2.5 seconds so the rocket hits the ground 25 seconds after it was launched at t=1