Question

Train 1 leaves point A at noon traveling due westaveraging 60 mph. Train 2 leaves point A at 1 p.m.,averaging 70 mph. How far apartwill the trains be on a straight line distance at 4 p.m. ?traveling due north

Answer 1

Given:

Speed of train 1 = 60 mph due west (leaves at noon).

Speed of train 2 = 70 mph (leaves at 1 pm).

Let's find how far apart they will be on a straigth line distance at 4 p.m.

We have:

• Time taken by train 1 = 4:00 - 12:00 = 4 hours

,

• Time taken by train 2 = 4:00 - 1:00 = 3 hours

Apply the formula:

Distance = speed x time

Thus, we have:

• Distance covered by train 1 = 60 x 4 = 240 miles

,

• Distance covered by train 2 = 70 x 3 = 310 miles

Now, to find how far apart, apply Pythagorean Theorem:

`\begin{gathered} BC=√(BA^2+AC^2) \\ \\ BC=√(240^2+210^2) \\ \\ BC=√(57600+44100) \\ \\ BC=√(101700) \\ \\ BC=318.9\text{ miles} \end{gathered}`

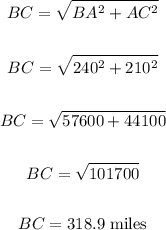
Therefore, the trains will be 318.9 miles apart on a straight line distance travelling due north.

• ANSWER:

318.9 miles