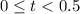Given the equation that represents this situation:
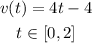
first, if we want to know when the yo-yo's velocity is greater than 2 feet per second, then:
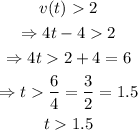
since t is defined between 0 and 2, the times for which the yoyo's velocity is greater than 2 feet per second is:
![1.5then, if we suppose that the velocity is less than -2 feet per second, then:[tex]\begin{gathered} v(t)<-2 \\ \Rightarrow4t-4<-2 \\ \Rightarrow4t<-2+4=2 \\ \Rightarrow t<(2)/(4)=(1)/(2)=0.5 \\ t<0.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ycpmt97pc19vbkxz442w58w43z8p9cr0y5.png)
then, we have that the interval is: