Question

Let the Universal Set, S, have 100 elements. A and B are subsets of S. Set A contains 49 elements and Set B contains 53 elements. If the total number of elements in either A or B is 78, how many elements are in A but not in B?

Answer 1

- The formula to apply for this question is:

`\text{Total elements in \lparen A or B \rparen = elements in A + elements in B - elements in \lparen A \& B \rparen}`

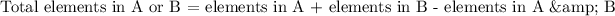
- We have been given:

`\begin{gathered} \text{ Total elements in \lparen A or B\rparen}=78 \\ \text{ elements in A}=49 \\ \text{ elements in B}=53 \end{gathered}`

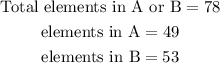
- Thus, we can apply the formula as follows:

`\begin{gathered} 78=49+53-X \\ 78=102-X \\ \text{ Subtract 102 from both sides} \\ \\ -X=78-102 \\ -X=-24 \\ \therefore X=24 \\ \\ \text{ This means that the number of elements in A and B }=24 \end{gathered}`

- Now that we know the number of elements in both sets A and B, we can find the number of elements that are in set A by simply subtracting the elements in both A and B from the total number of elements in set A.

- That is,

`\begin{gathered} \text{ elements in A only}=49-24 \\ \\ \therefore\text{ elements in A only}=25 \end{gathered}`

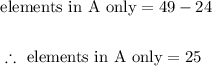
Final Answer

The answer is 25