Solution:
Given that:
In a sunflower seed head, there are 100 spirals going left.
Applying the golden ratio, i.e.
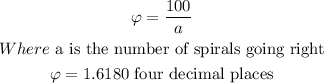
Substitute the value of the golden ratio to find the number of spirals going right, a.

Hence, the answer is 62 spirals (nearest whole number)