Step-by-step explanation:
We are given the following information;
A grocer wants to mix two types of candy, which we shall call x and y.
He wants to mix a total of 19 pounds which means, he would have the following;
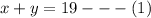
He also intends to sell the total mix for $1.55 per pound. At that rate, his total sales would be;

Note that one kind of candy sells for $1.30 per pound, that is;
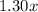
The other kind sells for $2.40 per pound, that is;
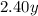
The total mix would now sell for;

We can now solve the system of equations and determine the values of x and y as follows;
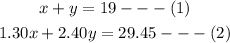
From equation (1), make x the subject of the equation and we'll have;
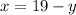
Substitute for the value of x into equation (2)
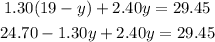
We can now combine like terms;

Divide both sides by 1.10;
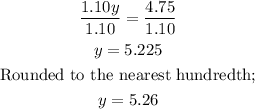
We can now substitute for the value of y into equation (1);
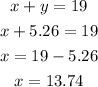
Therefore, he should use the following mix;
ANSWER:
For the $1.30 candy = 13.74 pounds
For the $2.40 candy = 5.26 pounds