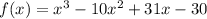
Test x = 2 and use it to find f(2) to and determine if (x-2) is factor of the polynomial f(x)
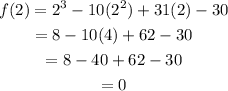
Since f(2) = 0, it means (x - 2) is a factor of the polynomial, let us show this with synthetic division
2 | 1 -10 31 -30
2 -16 30
1 -8 15 0
This shows that 2 is a zero.
Doing the same for 3 and 5, we have
3 | 1 -10 31 -30
3 -21 30
1 -7 10 0
Thus, 3 is also a zero.
For 5, we have,
5 | 1 -10 31 -30
5 -25 30
1 -5 6 0
Thus, 5 is also a zero.
The lower zeros is 2 while the upper zeros is 5