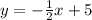Question

Write the slope intercept form of the equation of the described line:4) through: (4, 3), perp. to y = 2x + 4

Answer 1

To find the slope-intercept equation of a line, remember the general equation of a line in the slope-intercept form:

`y=mx+b`

Where m is the slope of the line and b is the y-intercept.

Notice that the equation y=2x+4 is written in the slope-intercept form. Therefore, its slope is 2.

For two lines to be perpendicular, their slopes should have a product of -1.

Since we are looking for a line perpendicular to y=2x+4, the slope of the desired line should be -1/2.

`m=-(1)/(2)`

Use the point-slope formula to find the line with slope -1/2 that goes through the point (4,3):

`y=m(x-x_0)+y_0`

Substitute m=-1/2, x_0=4 and y_0=3:

`y=-(1)/(2)(x-4)+3`

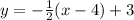
To find the slope-intercept form of this equation, use the distributive property to rewrite -1/2 (x-4) as -1/2 x -(1/2)(-4):

`y=-(1)/(2)x-(1)/(2)\cdot(-4)+3`

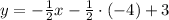
Simplify the product (-1/2)(-4):

`\begin{gathered} y=-(1)/(2)x+2+3 \\ \Rightarrow \\ y=-(1)/(2)x+5 \end{gathered}`

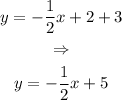
Therefore, the slope intercept form of the equation of a line perpendicular to y=2x+4 and which goes through the point (4,3), is:

`y=-(1)/(2)x+5`