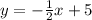To find the slope-intercept equation of a line, remember the general equation of a line in the slope-intercept form:

Where m is the slope of the line and b is the y-intercept.
Notice that the equation y=2x+4 is written in the slope-intercept form. Therefore, its slope is 2.
For two lines to be perpendicular, their slopes should have a product of -1.
Since we are looking for a line perpendicular to y=2x+4, the slope of the desired line should be -1/2.
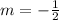
Use the point-slope formula to find the line with slope -1/2 that goes through the point (4,3):

Substitute m=-1/2, x_0=4 and y_0=3:
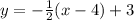
To find the slope-intercept form of this equation, use the distributive property to rewrite -1/2 (x-4) as -1/2 x -(1/2)(-4):
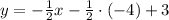
Simplify the product (-1/2)(-4):
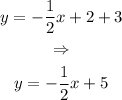
Therefore, the slope intercept form of the equation of a line perpendicular to y=2x+4 and which goes through the point (4,3), is: