Given the series below
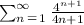
By the limit comparison test, the series diverges
Hence, the series diverges
Where
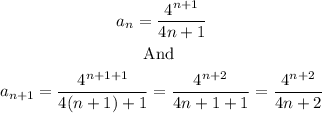
For the ratio test,

Substitute for the series
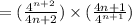
Solve
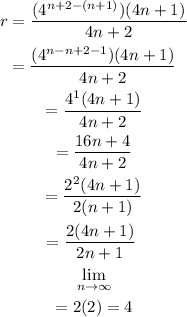
The value of r from the ratio test is 4
Since r is greater than 1 i.e r > 1
Hence, the series diverges