ANSWER/EXPLANATION:
(1) We shall take the following as an example of a rational function;
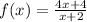
(2) This function has an asymptote at the point where the denominator equals zero, that is;
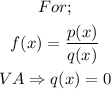
For this function the vertical asymptote (V.A) would be;
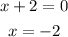
At the point where x = -2, the graph moves very close (almost touches) to x = -2 but never touches it.
(3) To determine if there is a hole in this graph, we need to find any input value at which both the numerator and denominator equals zero.
For this rational function we shall begin by factoring both numerator and denominator;
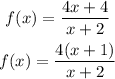
There are no common factors for the numerator and denominator, hence there is no hole in this graph.
However, we can take another example;
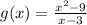
If we factor the numerator we would have;

Note that;

Is common to both numerator and denominator. For this factor;
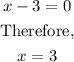
There is a hole at the point where x = 3