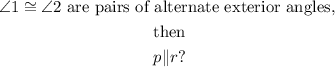Question

Fill in the missing statements and reasons in each proof shown below. You must mark the diagram for

Answer 1

a) Statement

`g\mleft\Vert h\mright?`

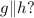
Reason - Given.

It has been stated and given in the question.

b) Statement

`\angle1\cong\angle3`

Reason - Corresponding angles

Corresponding angles are the pairs of angles that are found in the same relative position on different intersections.

c) Statement

`\angle1\cong\angle2`

Reason - Given.

It has been stated and given in the question.

d) Statement

`\angle2\cong\angle3`

Reason - Transitive property of congruency

The transitive property of congruence states that two objects that are congruent to a third object are also congruent to each other.

i.e. if a = b and b = c, then a = c

Since,

`\begin{gathered} \angle1\cong\angle3 \\ \text{and} \\ \angle1\cong\angle2 \\ \text{Then,} \\ \angle2\cong\angle3 \end{gathered}`

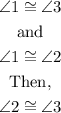
e) Statement

`p\mleft\Vert r\mright?`

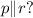
Reason - Converse of alternate exterior angle

The converse of alternate exterior angle theorem states that, if the alternate exterior angles formed by two lines, which are cut by a transversal, are congruent, then the lines are parallel.

Since,

`\begin{gathered} \angle1\cong\angle2\text{ are pairs of alternate exterior angles, } \\ \text{then} \\ p\mleft\Vert r\mright? \end{gathered}`