The exponential regression model that fits the data is;
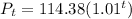
(b) In 2040;
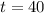
Thus, the model predicts that the population of mexico will be;
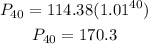
The model predicts that the population of mexico will be 170.3 million people.
(c) When the population of mexico reach 145 million, the year will be;
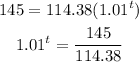
So, we have;
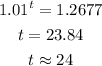
During the year 2024.