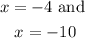Question

Please help me with this problem. Solve for x.0 = x² + 14x + 40Enter your answers in the boxes.The solutions are and .

Answer 1

We are given the following equation;

`x^2+14x+40=0`

This is a quadratic equation and to solve this we would group the entire expression on the left side of the equation. Note that we can use what is usually refered to as rthe "sum/product" rule.

We break down 40 into two factors and those two factors must sum up to 14, that is;

`\begin{gathered} a* b=40\text{ (product)} \\ a+b=14\text{ (sum)} \end{gathered}`

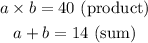
Next, we observe that the factors of 40 which also sum up to 14 are

`10,4`

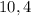
We can now split 14x as follows;

`x^2+10x+4x+40=0`

Next step, we group them into twos and factorize;

`(x^2+10x)+(4x+40)=0`

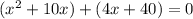
Factorize each group;

`x(x+10)+4(x+10)=0`

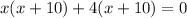
Notice that both parenthesis are the same expression. We can now take that as one factor and take the other two values (that is, x and 4) as the other factor.

`(x+4)(x+10)=0`

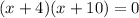
We can now solve both factors separately, as follows;

`\begin{gathered} x+4=0 \\ x=-4 \\ \text{Also,} \\ x+10=0 \\ x=-10 \end{gathered}`

Therefore, the solutions are;

ANSWER:

`\begin{gathered} x=-4\text{ and } \\ x=-10 \end{gathered}`