ANSWER
The roots are unequal and real.
Step-by-step explanation
To find the nature of the roots of the equation, we have to find the discriminant using the formula:
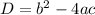
where a = coefficient of x² = 1
b = coefficient of x = -1
c = constant term = -20
Therefore, the discriminant is:
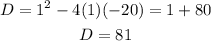
Since the discriminant is greater than 0, the roots are unequal and real.