Question

I need to find a four degree polynomial function based on the graph in the picture

Answer 1

`f(x)\text{ = }(1)/(6)(x\text{ + 3)(x + 1)(x - 1)(x - 2)}`

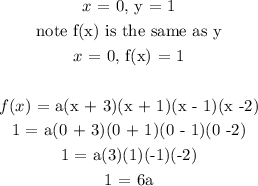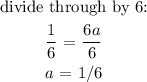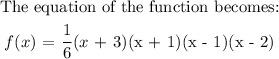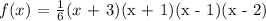
Step-by-step explanation:

To write an equation using a polynomial graph, first we need to find the x intercepts

x-intercepts are the values of x when y = 0.

On the graph, these are values of x when the line crosses or touches the x axis

from the graph:

The line touches/crosses the x axis at x = -3, -1, 1, 2

So, x intercepts are x = -3, -1, 1, 2

Next, we will check if there is multiplicity. This means we check if at any of the x intercept, the line the cross the x axis.

In our graph, all the line passing the x-intercepts cross the x axis so no multiplicity

We need to get the factors from the x intercepts:

x = -3 will become (x + 3)

x = -1 will become (x + 1)

x = 1 will become (x - 1)

x = 2 will become (x - 2)

The equation of the graph will be in the form:

`\begin{gathered} f(x)\text{ = a(x + 3)(x + 1)(x - 1)(x -2)} \\ \text{where a = elasticity (or the multiplying factor that }\det er\min es\text{ its stretch or compression)} \end{gathered}`

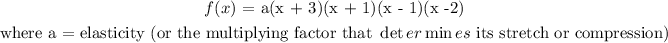
To determine a, we will pick a point on the graph and substitute in the equation we got above

Most often the y intercept is used in this case.

The y-intercept is value of y when the line crosses the y axis on a graph

The y-intercept on the graph is y = 1

In orderd form: (0, 1)

substitute in the equation:

`\begin{gathered} x\text{ = 0, y = 1} \\ \text{note f(x) is the same as y} \\ x\text{ = 0, f(x) = 1} \\ \\ f(x)\text{ = a(x + 3)(x + 1)(x - 1)(x -2)} \\ 1\text{ = a(0 + 3)(0 + 1)(0 - 1)(0 -2)} \\ 1\text{ = a(3)(1)(-1)(-2)} \\ 1\text{ = 6a} \end{gathered}`
`\begin{gathered} \text{divide through by 6:} \\ (1)/(6)\text{ = }(6a)/(6) \\ a\text{ = 1/6} \end{gathered}`
`\begin{gathered} \text{The equation of the function becomes:} \\ f(x)\text{ = }(1)/(6)(x\text{ + 3)(x + 1)(x - 1)(x - 2)} \end{gathered}`