Question

I need help for these two questions. For the second graph I just need to find the domain and range of f^-1(x)

Answer 1

Notice that the left side of the graph corresponds to y=-x, whereas the right side corresponds to another line. We can find the former by simply using two points. In this case (0,0) and (5,-3).

Then the equation of the line on the right side is:

`y=-(3)/(5)x`

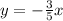
So, the function is:

`y=f(x)=\begin{cases}-x;-7\le x\le0 \\ -(3)/(5)x;0\le x\le5\end{cases}`

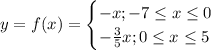
Since function f(x) has two parts, so does the inverse function.

Remember the definition of an inverse function, let g(x) be a function:

`\begin{gathered} g^(-1)\circ g(x)=x, \\ g\circ g^(-1)(y)=y \end{gathered}`

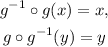
As for the left side of the function:

`\begin{gathered} f^(-1)\circ f(x)=x \\ andf^(-1)\circ f(x)=f^(-1)(-x) \\ \Rightarrow f^(-1)(-x)=x \\ \Rightarrow f^(-1)(x)=-x \end{gathered}`

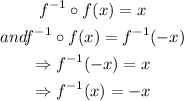
Now, the right side:

`\begin{gathered} f^(-1)\circ f(x)=x \\ \Rightarrow f^(-1)\circ f(x)=f^(-1)(-(3)/(5)x) \\ \Rightarrow f^(-1)(-(3)/(5)x)=x \\ \Rightarrow f^(-1)(x)=-(5)/(3)x \end{gathered}`

Thus, the inverse function is:

`f^(-1)(x)=\begin{cases}-x,-7\le x\le0 \\ -(5)/(3)x,0\le x\le5\end{cases}`

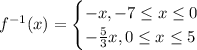
The range of the inverse function is:

For the first part of the function:

`range(f^(-1)(x))=\begin{cases}f(x)\in\lbrack0,7\rbrack,x\in\lbrack-7,0\rbrack \\ f(x)\in\lbrack-(25)/(3),0\rbrack,x\in\lbrack0,5\rbrack\end{cases}`

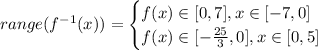
Merging both results:

`\begin{gathered} range(f^(-1)(x))=\lbrack-(25)/(3),7\rbrack \\ domain(f^(-1)(x))=\lbrack-7,5\rbrack \end{gathered}`