Question

If cos(0)= -1/sqrt5, what are possible values of sin(0)?

Answer 1

To solve this, we can use the following trigonometric identity:

`\sin ^2\theta+\cos ^2\theta=1`

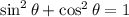
By replacing 0 for θ, we get:

`\sin ^2(0)+\cos ^2(0)=1`

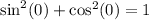
by replacing -1/sqrt5 for cos(0), we get:

`\begin{gathered} \sin ^2(0)+(-\frac{1}{\sqrt[]{5}})^2=1 \\ \sin ^2(0)+\frac{(-1)^2}{(\sqrt[]{5)^2}}^{}=1 \\ \sin ^2(0)+\frac{1^{}}{5^{}}^{}=1 \end{gathered}`

From this equation, we can solve for the sin(0), like this:

`\begin{gathered} \sin ^2(0)+\frac{1^{}}{5^{}}^{}=1 \\ \sin ^2(0)+\frac{1^{}}{5^{}}^{}-(1)/(5)=1-(1)/(5) \\ \sin ^2(0)+0=1*(5)/(5)-(1)/(5) \\ \sin ^2(0)=(5)/(5)-(1)/(5) \\ \sin ^2(0)=(5-1)/(5) \\ \sin ^2(0)=(4)/(5) \\ \sqrt[]{\sin ^2(0)}=\sqrt[]{(4)/(5)} \\ \sin (0)=\pm\sqrt[]{(4)/(5)} \\ \sin (0)=\pm\frac{\sqrt[]{4}}{\sqrt[]{5}}=\pm\frac{2}{\sqrt[]{5}}= \end{gathered}`

Then, the posible values of sin(0) are 2/sqrt(5) and -2/sqrt(5)