Given:
a.) An orchard has 744 orange trees.
b.) The number of rows exceeds the number of trees per row by 7.
In this type of scenario, we will be using the following formula:
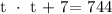
Where,
t = the number of trees in each row
We get,
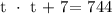
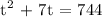
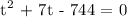
Let's find t using the quadratic formula:
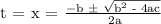
Where, a = 1 , b = 7 and c = -744
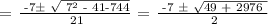
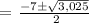
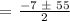
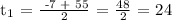
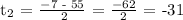
It should never be a negative number, therefore, the answer should be t = 24.
Thus, there should be 24 trees in each row.