In this problem, we need to apply systems of equations to buying Cat Trees.
We are given to companies with different conditions, so we can write these equations.
Part [A]
One company, PP, offers the following deal:
- $100 for the cat tree,
- and $50 for each additional part or toy.
The second company, MN, offers this deal:
- $50 for a basic cat tree
- $75 for each additional part
For both companies, let x represent the additional pieces and y represent the total cost. Then we get

Part [C]
One way to solve this system is by graphing the equations. We can do this by creating a simple table for each function, then graph the points. Which numbers this large, a table is the better way to go.
Let's begin with the company PP:
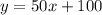
A simple table gives us
Graphing those points, we have:
Next, we move on to the company MN:
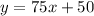
We can create a similar table and graph it on the same coordinate plane.
Part [D]
Finally, we want to talk about someone trying to decide the best place to purchase the cat tree depending on how many add-on's he want to buy.
Based on the graph, we see that the cat trees will cost the same if he buys 2 add-ons.
If he chooses to buy less than 2 add-ons, the MN company wil give the cheaper prices (in blue).
If he wants to buy more than 2 add-ons, the PP company will get him the cheaper overall cost.