To solve the exercise you can use proportions, like this:
*For the length
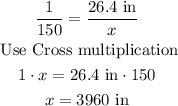
*For the height
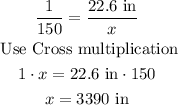
Then, the actual size of the ship is 3960 inches in length and 3390 inches in height.
Now, to convert these measurements to feet, you can use the proportion:
*For the length
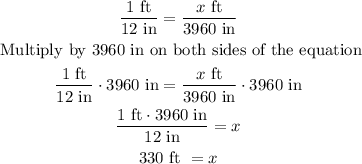
*For the height:
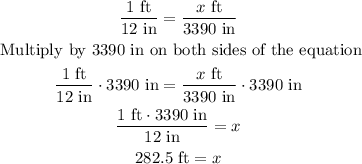
Therefore, the actual size of the ship is 330 feet in length and 282.5 feet in height.