Question

EFind the surface area and volume of the solid produced by rotating the figure around the given axis. Round each answer to the nearesthe surface area of the solid is aboutsquare units and the volume of the solid is aboutcubic units

Answer 1

1) S= 9pi +24 units² 2) V=18pi u³

Since the figure is made of a rectangle, and a quarter of a circle,

then Let's calculate it by parts.

1) The surface of the rectangular part

`\begin{gathered} S=8\cdot3 \\ S=24 \end{gathered}`

2) Given the fact the we need 1/4 of the area of a circle. So:

`\begin{gathered} S_1=\pi.(3)^2 \\ S_c=9\pi \end{gathered}`

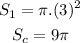
Finally, The surface area of the solid is about 9pi +24

The Volume:

Considering that the rectangle, rotating produces a solid called cylinder

and that a quarter of a circle rotated around the x produces a hemisphere

Let's calculate it

Volume of the cylinder

`\begin{gathered} V=\pi.r^2.h \\ V=\pi.(3)^2.8 \\ V=72\pi \end{gathered}`

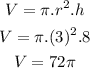
And the Volume of the hemisphere (half of the volume of a sphere)

`\begin{gathered} V=(1)/(2)\cdot(4\pi(3)^(3))/(3) \\ V=(4\pi27)/(6) \\ V=18\pi \end{gathered}`

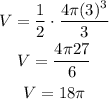
And the Volume of the solid is about 90 pi