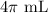1 Answer

Ask a Question

Mark Story · Answer 1 · 2023-03-24T02:21:30+0000

A straw is cylindrical in nature.

The amount of liquid that a structure can hold is the volume.

Thus, we find the volume of the cylinder.

Given:

All units must be the same, so we convert them to be in the same unit of length.

$\begin{gathered} \text{length of straw = height of straw = h = 25cm} \\ \text{diameter of straw = }d\text{ = 8mm} \\ 1\operatorname{mm}=0.1\operatorname{cm} \\ 8\operatorname{mm}=0.1*8=0.8\operatorname{cm} \\ d=0.8\operatorname{cm} \\ \text{radius is half of diameter} \\ r=(d)/(2) \\ r=(0.8)/(2) \\ r=0.4\operatorname{cm} \end{gathered}$

The volume of a cylinder is given by;

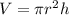
$V=\pi r^2h$
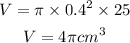
$\begin{gathered} V=\pi*0.4^2*25 \\ V=4\pi cm^3 \end{gathered}$

The volume in terms of pi is

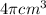
$4\pi cm^3$

To convert the volume to mL,

$1\operatorname{cm}^3=1mL$

Therefore,

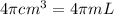
$4\pi cm^3=4\pi mL$

Therefore, the straw can contain 4 pi mL of liquid.

Volume =

$4\pi\text{ mL}$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions