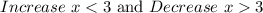Step-by-step explanation:
We are given a parabola which opens downwards as shown in the question.
To determine the intervals over the graph/function increases and decreases, we will need to study carefully the movement of the graph along the y-axis. As the graph rises along the y-axis, the corresponding x-values of the increasing region will be our intervals. The same procedure will be used to determine the interval of decrease.
Let us now study the movements of the curve;
Notice that the graph rises and reaches a maximum at the point where;

This means it rises from all x values less than 3 and does not rise beyond 3. Therefore;
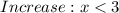
After that it begins to fall continuously. That means the graph decreases at every x value after 3, that is;
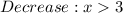
Therefore,
ANSWER: