Given:
Team X has a 40% chance of winning a game against team Y and team A has a 25% chance of winning a game against team B.
Required:
What is the probability of team X and team A winning their respective games?
Step-by-step explanation:
The concept required:

So,
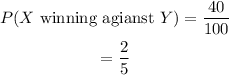
And
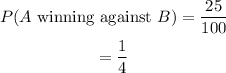
Answer:
Completed the answer.