Question

Two connected gears are rotating. The smaller gear has a radius of 4 inches, while the larger gear has a radius of 7 inches. What is the angle through which the larger gear has rotated when the smaller gear has completed one full rotation? Answer in radians and degrees. 7 in 4 In

Answer 1

When there are connected gears, the arc lenght must be equal. That is:

When the smaller gear has completed one full rotation, we have

`\theta_2=2\pi`

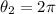
since R=7in and r=4 in, we have that

`7\cdot\theta_1=4\cdot2\pi`

and we must isolate theta_1. Hence, the answer in radians is

`\theta_1=(8\pi)/(7)\text{ radians}`

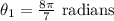
Now, we must convert radians to degrees. This can be given by applyng the rule of three:

`\begin{gathered} \pi\text{ radian ----180 degre}es \\ (8\pi)/(7)\text{ radian ---- x} \end{gathered}`

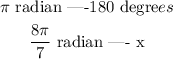
therefore, x is equal to

`\begin{gathered} x=((8\pi)/(7)\cdot180)/(\pi) \\ x=(8\pi\cdot180)/(7\cdot\pi) \\ x=(8\cdot180)/(7) \\ x=(1440)/(7) \\ x=205.71\text{ degr}ees \end{gathered}`

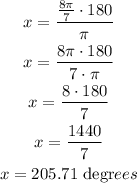
hence, in degrees the answer is 205.71 degrees