Step-by-step explanation:
The equations are given below as
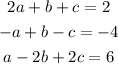
isolate a in equation (1) to give
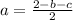
Susbtitute the equation of a in equation (2) and (3)
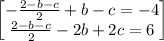
Simplifying the equation, we will have
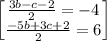
Isolate b from the equation below
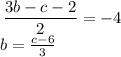
substiuting , we will have
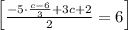
On simplifying , we will have
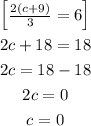
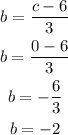
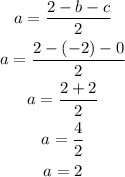
Hence,
The final answers are
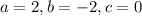
The final answer is