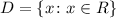Question

Please help me on my question It’s all one question

Answer 1

Since the given functions are

`f(x)=(2)/(x),g(x)=3x+12`

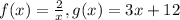
To find f(g(x)), substitute x in f by g(x)

`(f\circ g)(x)=(2)/(3x+12)`

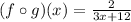
The domain is the values of x that make the function defined

The function is undefined if the denominator = 0

Then equate the denominators by 0 to find the values of x which make the denominator = 0

`\begin{gathered} x=0 \\ 3x+12=0 \\ 3x+12-12=0-12 \\ 3x=-12 \\ (3x)/(3)=-(12)/(3) \\ x=-4 \end{gathered}`

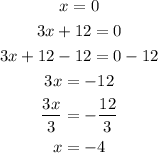
Then the domain is all values of x except {-4, 0}

`D=\mleft\lbrace x\colon x\in R,x\\e-4,0\mright\rbrace`

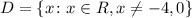
To find g(f(x)), substitute x in g by f(x)

`\begin{gathered} (g\circ f)(x)=3((2)/(x))+12 \\ (g\circ x)=(6)/(x)+12 \end{gathered}`

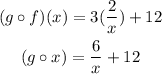
The domain of it is all values of x except x = 0

`D=\mleft\lbrace x\colon x\in R,x\\e0\mright\rbrace`

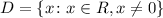
To find f(f(x)), substitute x in f by f(x)

`\begin{gathered} (f\circ f)(x)=(2)/((2)/(x)) \\ (f\circ f)(x)=2*(x)/(2) \\ (f\circ f)(x)=x \end{gathered}`

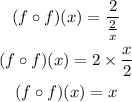
The domain of it is all values of x except x = 0

`D=\mleft\lbrace x\colon x\in R,x\\e0\mright\rbrace`

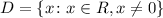
To find g(g(x)), substitute x in g by g(x)

`(g\circ g)(x)=3(3x+12)+12`

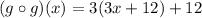
Simplify it

`\begin{gathered} (g\circ g)(x)=3(3x)+3(12)+12 \\ (g\circ g)(x)=9x+36+12 \\ (g\circ g)(x)=9x+48 \end{gathered}`

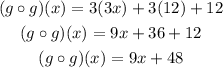
Since there is no denominator in this function, then

The domain is all values of x

`D=\mleft\lbrace x\colon x\in R\mright\rbrace`