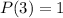Solution:
The remainder theorem states that when P(x) is divided by x-a, then the remainder is P(a).
From the graph of P(x) given, if we divide it by x-3,

To get the remainder, we look at the graph.
The remainder P(3) from the graph means the value of y, when x = 3
By inspection, the value of y when x = 3 from the graph is 1.
This is as shown in the graph below;
Hence, the remainder which is P(3) is the point marked red on the graph.
This corresponds to y = 1
Therefore, the remainder is;