Given:
The graph of the function
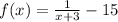
is a transformation of the graph of
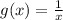
Required:
Find the vertical and the horizontal shift of units.
Step-by-step explanation:
The graph of
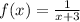
shift the graph of
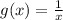
left 3 units by subtracting 3 from the x-coordinates of the points on the graph of 1/x.
The graph of
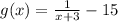
shift the graph of
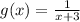
down 15 units by subtracting 15 from the y-coordinates of the points on the graph of
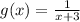
Thus the graph
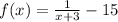
shift the graph of
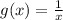
horizontal left 3 units and the vertical shift down 15 units.
Final Answer:
Vertical shift - down 15 units
Horizontal shift - left 3 units