Question

The value of a machine, V, at the end of t years is given by V = C(1 - r)^t where C is the original cost and r is the rate of depreciation. Find the value of a machine atthe end of 3 years if the original cost was $1963 and r = 0.2. Round to the nearest cent.

Answer 1

We need to find the value V of a machine, given by:

`V=C(1-r)^t`

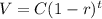
where C is the original cost, t is the number of years, and r is the rate of depreciation.

For this problem, we have:

`\begin{gathered} C=\text{ \$}1963 \\ r=0.2 \\ t=3 \end{gathered}`

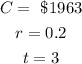
Then, using the above information in the formula, we obtain:

Therefore, rounding to the nearest cent, we obtained:

Answer: $100.06