Given:
The principal value is P = 305,000.
The annual interest rate is r = 7.8%.
The time period is t = 5 years.
Step-by-step explanation:
The formula of equally monthly installment is,
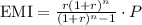
Here, n is number of months, P is principal value and t is monthly rate of interest.
Determine the number of months in 25 years.
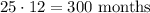
The monthly interset rate is,
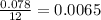
Substitute the values in the formula to determine the equation for equally monthly installments.
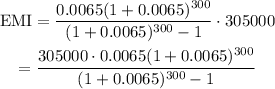
Option D is correct.