Given data:
* The current through the system is I = 3 A.
* The resistance of resistors connected in parallel is,
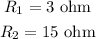
Solution:
The equivalent resistance of the system is,
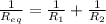
Substituting the known values,
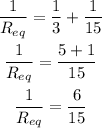
By taking inverse value,
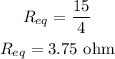
According to Ohm's law, the voltage across the battery is,
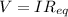
Substituting the known values,
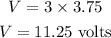
Thus, the voltage across the battery is 11.25 volts.