Question

Which system is represented in the graph? y > x2 + 4x – 5y > x + 5 y < x2 + 4x – 5y < x + 5 y ≥ x2 + 4x – 5y ≤ x + 5 y > x2 + 4x – 5y < x + 5

Answer 1

The given parabola has a vertex of (-2,-9), in vertex form the equation of the parabola is

`\begin{gathered} y=(x-h)^2+k \\ \text{where} \\ (h,k)\text{ is the vertex} \\ \; \\ y=(x-h)^(2)+k \\ y=(x-(-2))^2+(-9) \\ y=(x+2)^2-9 \\ \text{Expand the binomial and simplify} \\ y=(x^2+4x+4)-9 \\ y=x^2+4x-5 \end{gathered}`

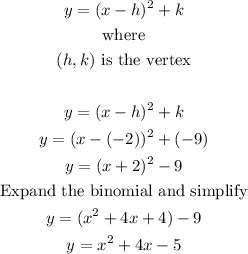
Since the shaded area of the parabola is in the top part, and uses a dashed line, the inequality therefore is

`y>x^2+4x-5`

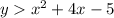
The linear inequality has a slope of 1, and a y-intercept of 5, which means that its linear equation is

`y=x+5`

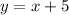
The same as the previous graph, since it has a shaded region in the top part and uses the dashed line, the linear inequality is

`y>x+5`

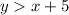
Therefore, the graph is represented by the system

`\begin{cases}y>x^2+4x-5 \\ y>{x+5}\end{cases}`