the Given data:
Initial volume;
![V_1=130\operatorname{cm}^3]()
Initial pressure;
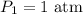
Final volume;
![V_2=40\operatorname{cm}^3]()
According to ideal gas equation;
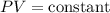
Therefore,
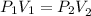
Here, P_2 is the final pressure.
The final pressure is given as,
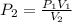
Substituting all known values,
![\begin{gathered} P_2=\frac{(1\text{ atm})*(130\operatorname{cm})}{(40\operatorname{cm}^3)} \\ =3.25\text{ atm} \end{gathered}]()
Therefore, the new pressure inside the pump is 3.25 atmospheres.