1 Answer

CyberGuy · Answer 1 · 2023-03-25T20:17:56+0000

the Given data:

Initial volume;

$V_1=130\operatorname{cm}^3$

Initial pressure;

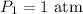
$P_1=1\text{ atm}$

Final volume;

$V_2=40\operatorname{cm}^3$

According to ideal gas equation;

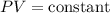
$PV=\text{constant}$

Therefore,

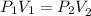
$P_1V_1=P_2V_2^{}$

Here, P_2 is the final pressure.

The final pressure is given as,

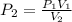
Substituting all known values,

$\begin{gathered} P_2=\frac{(1\text{ atm})*(130\operatorname{cm})}{(40\operatorname{cm}^3)} \\ =3.25\text{ atm} \end{gathered}$

Therefore, the new pressure inside the pump is 3.25 atmospheres.

Please log in or register to add a comment.