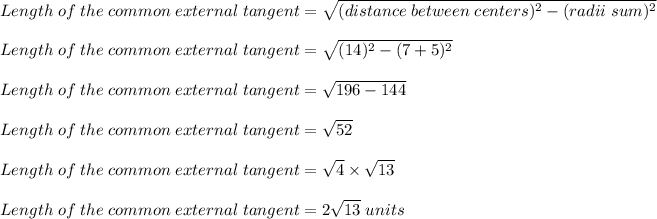Since the centers of two circles with radii 5 and 7 are 14 units apart, the length of the common external tangent is equal to
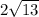 units.
units.
In Mathematics and Geometry, Pythagorean theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

Where:
- a is the opposite side of a right-angled triangle.
- b is the adjacent side of a right-angled triangle.
- c is the hypotenuse of a right-angled triangle.
In order to determine the length of the common external tangent, we would have to apply Pythagorean's theorem as follows;