Question

Please check out with the first question ( question 4) it’s geometry

Answer 1

The diagram showing the setup in the question is shown below:

We can use the Pythagorean Theorem to solve for the length of the rope:

`\begin{gathered} c^2=a^2+b^2 \\ where\text{ c is the hypotenuse and a and b are the other two sides} \end{gathered}`

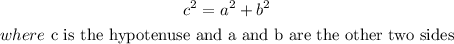
From the diagram, we have the following parameters:

`\begin{gathered} c=x \\ a=6 \\ b=11 \end{gathered}`

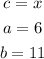
Therefore, the length of the rope is calculated to be:

`\begin{gathered} x^2=6^2+11^2 \\ x^2=36+121 \\ x^2=157 \\ x=√(157) \\ x=12.5 \end{gathered}`

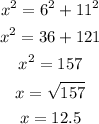
The length of the rope is 12.5 meters.