Answer:
A. (6, 0)
Step-by-step explanation:
The starting location that would have the steepest average rate of change will be the starting point such that this point and the location of the building (2,6) has the greatest slope.
So, the slope of a line that passes through the points (x1, y1) and (x2, y2) is:

Therefore, the slope of a line that passes through (2, 6) and (6, 0) is:
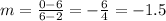
The slope of a line that passes through (2, 6) and (-1, 2) is:
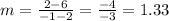
The slope of a line that passes through (2, 6) and (-3, -1) is:
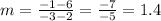
The slope of a line that passes through (2, 6) and (7, 1) is:
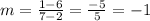
Since 1.5 is the greatest slope, the starting location with the steepest average rate of change is A. (6, 0)