Answer:
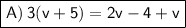
Explanation:
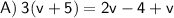
Combine like terms:
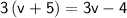
Expand:
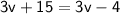
Subtract 15 from both sides:
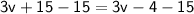
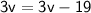
Subtract 3v from both sides:
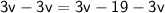


_________________
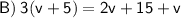
Combine like terms:
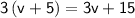
Expand:
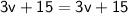
Subtract 15 from both sides:
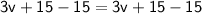

Subtract 3v from both sides:
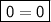
_______________________
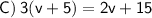
Expand:
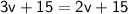
Subtract 15 from both sides:
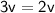
Subtract 2v from both sides:
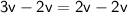
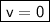
_______________________
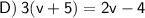
Expand:
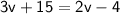
Subtract 15 from both sides:
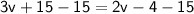
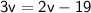
Subtract 2v from both sides:
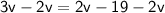

___________________________