Question

The first line in a system of linear equations has a slope of 2 and passes through the point (1, -1). The second line passes through the points (8,-5) and (10, -10). What is the solution to the system?

Answer 1

Solving for the equation of the first line

Given: slope of 2, and passes through point (1,-1)

Recall the point slope form of a line

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where} \\ m\text{ is the slope} \\ (x_1,y_1)\text{ is the point in the line} \end{gathered}`

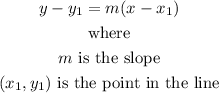
Substituting the given, and solving in terms of y, the equation of the first line is

`\begin{gathered} y-(-1)=2\lbrack x-(1)\rbrack \\ y+1=2(x-1) \\ y+1=2x-2 \\ y=2x-2-1 \\ y=2x-3 \end{gathered}`

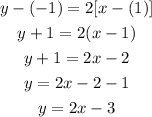
Solving for the equation of the second line

Given: points (8,-5) and (10,-10)

First solve for the slope of the line

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(-10-(-5))/(10-8) \\ m=(-10+5)/(2) \\ m=-(5)/(2) \end{gathered}`

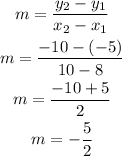
Now that we have the slope, use the point-slope form and solve in terms of y to get the equation of the second line

`\begin{gathered} \text{Using the point (10,-10) we have} \\ y-(-10)=-(5)/(2)(x-10) \\ y+10=-(5)/(2)x+25 \\ y=-(5)/(2)x+25-10 \\ y=-(5)/(2)x+15 \end{gathered}`

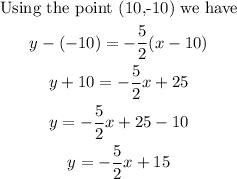
Solving for the solution of the system

Now that we have two equations

`\begin{cases}y=2x-3 \\ y=-(5)/(2)x+15\end{cases}`

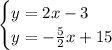
Equate both y's, substitute, and solve for x

`\begin{gathered} y=y \\ 2x-3=-(5)/(2)x+15 \\ \\ \text{Multiply both sides by }2,\text{ to get rid of fractions in the right side of equation} \\ \Big(2x-3\Big)\cdot2=\Big(-(5)/(2)x+15\Big)\cdot2 \\ 4x-6=-5x+30 \\ \\ \text{Add both sides by }5x+6 \\ 4x-6=-5x+30 \\ 4x+5x-6+6=-5x+5x+30+6 \\ 9x\cancel{-6+6}=\cancel{-5x+5x}+36 \\ 9x=36 \\ \\ \text{Divide both sides by }9 \\ 9x=36 \\ (9x)/(9)=(36)/(9) \\ x=4 \end{gathered}`

Now that we have solved for x, substitute the value to get the solution for y

Use either of the two equation, in this instance we will be using the first equation (using the second equation will work just as well)

`\begin{gathered} y=2x-3 \\ y=2(4)-3 \\ y=8-3 \\ y=5 \end{gathered}`

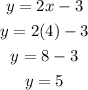
With x = 4, and y = 5, the solution to the system therefore is (4,5).