ANSWER
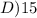
Step-by-step explanation
We want to find the distance between the two points given: (2, -6) and (-7, 6)
To do that, we will apply the formula for distance between two points:
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
where (x₁, y₁) and (x₂, y₂) are the two points.
We have that:

Therefore, the distance between them is:
![\begin{gathered} d=\sqrt[]{(-7-2)^2+(6-(-6))^2}=\sqrt[]{(-9)^2_{}+(6+6)^2} \\ d=\sqrt[]{(-9)^2+(12)^2}=\sqrt[]{81+144} \\ d=\sqrt[]{225} \\ d=15 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mmpfbtvyfmkm127o76zirhta1sow68b1vr.png)
That is the distance between the two points.