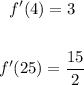Given the function:
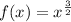
You can rewrite it in this form:
![f(x)=\sqrt[]{x^3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/b8zt3s6krtdiiycb051npau9yewwrhqqsd.png)
Because by definition:
![\sqrt[n]{b^m}=b^{(m)/(n)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/u5iqexyf0j58pvqeahuamadrboiv2xqrp6.png)
• The formula for calculating the Average Rate of Change over an interval is:
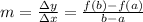
Where these two points are on the function:
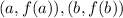
In this case, given the interval:
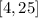
You can identify that:
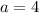
Then, substituting this value into the function and evaluating, you get:
![f(a)=f(4)=\sqrt[]{(4)^3}=\sqrt[]{64}=8](https://img.qammunity.org/2023/formulas/mathematics/high-school/8wf78t8w0z6hjayc7x57oq0rylann9yp7f.png)
You can also identify that:
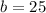
Then, substituting this value into the function and evaluating, you get:
![f(b)=f(25)=\sqrt[]{(25)^3}=125](https://img.qammunity.org/2023/formulas/mathematics/high-school/dtd3euye0xm8my70q1x2o42xh6ldnzyzjw.png)
Now you can substitute values into the formula and then evaluate, in order to find the Average Rate of Change over the given interval:

• In order to find the Instantaneous Rate of Change at the endpoints of the interval, you need to:
1. Derivate the function. Then, you need to find:
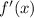
By definition:
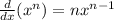
Therefore, applying this rule, you get:
![(dy)/(dx)(x^{(3)/(2)})=(3)/(2)x^{(3)/(2)-1}=(3)/(2)x^{(3)/(2)-1}=(3)/(2)x^{(1)/(2)}=(3)/(2)\sqrt[]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/u8xr05aa8yx871slmbvwzhad0elgau022z.png)
Then:
![f^(\prime)(x)=(3)/(2)\sqrt[]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/olmc789g8tkmokx6u2w02abjajnby1ppyb.png)
2. Now you have to substitute this value of "x" into the function derivated:

In order to find:
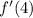
Then, substituting and evaluating, you get:
![\begin{gathered} f^(\prime)(4)=(3)/(2)\sqrt[]{4} \\ \\ f^(\prime)(4)=(3)/(2)\sqrt[]{4} \\ \\ f^(\prime)(4)=3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wo70yunzxch8ovvvrerxle94lp1465c8fn.png)
3. Substitute this value of "x" into the function derivated before:
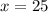
In order to find:

Then, substituting and evaluating, you get:
![\begin{gathered} f^(\prime)(25)=(3)/(2)\sqrt[]{25} \\ \\ f^(\prime)(25)=(15)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/e322py4586cm4cqz51f6sajhszyvfqujvr.png)
Hence, the answers are: